Vance J. Van Doren'in Control Engineering dergisi Kasım/Aralık 2003 sayısında yayınlanan "Loop Tuning Fundamentals" başlıklı yazısından çevrilmiştir. İlgilenenler sorularını bu sitedeki formlarla veya e-posta kanalıyla iletebilirler.
okul@metroloji.com.tr
PID - ÇEVRİM AKORTLAMAYA GİRİŞ
PID-çevrimlerini akortlamak (parametreleri iyi belirlemek), sihirbazlık gerektirmeyebilir ama bu işin incelikleri, bilim ile sanat arasında bir yerlerdedir. Bu yazıdaki kanıtlanmış akortlama ipuçları, proseslerinizi son haline getirmek için yardımcı olabilir.
Bir kontrol çevrimi, istenen set noktası ile ölçülen bir proses değişkeni arasındaki farkı gidermeye çalışan bir geribesleme mekanizmasıdır. Denetimci, proses değişkenini aşağı veya yukarı zorlayabilen mekanizmalar vasıtasıyla gerekli düzeltici hareketleri uygular.
Bir oransal-integral-türev (PID) denetimcisi, set noktası ve proses değişkeni arasındaki hatayı, önceki hataların integralini (toplamını), ve hatanın hangi oranda değişmekte olduğunu izler. Bir sonraki düzeltici hareketini bu üç terimin (veya modun) ağırlıklı toplamından hesaplar, sonra sonuçları prosese uygular ve ölçümü bekler.
PID temelleri
İdeal veya ISA standart formundaki PID algoritmasını kullanan bir PID denetimci, CO(t) çıkışını Şekil 1'de görülen formüle göre hesaplar. PV(t), t zamanında ölçülen proses değişkenini, ve hata e(t) ise set noktası ile proses değişkeni arasındaki farkı gösterir. PID formülü oransal terimin ağırlığını P faktörü ile, integral teriminkini P/Ti faktörü ile, türev terimininkini PTd faktörü ile belirler. Burada P, denetimci kazancını, Ti integral zamanını, Td ise türev zamanını ifade etmektedir.
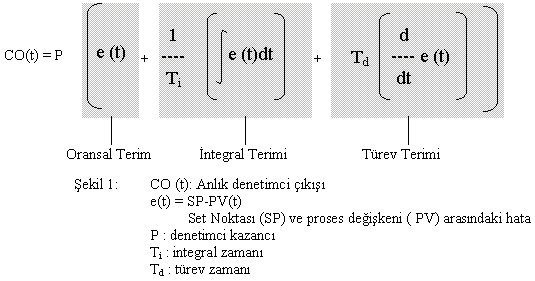
Bu terminolojiyi açıklayacak olursak;
Hata sinyali, denetimci çıkışının bir parçası olmak üzere denetimciden geçerken, kuvvetindeki artış veya azalma miktarına kazanç diyoruz. Yüksek kazançlı bir PID denetimcisi, hataları gidermek için fazlasıyla etkili düzeltme hareketleri yapmaya eğilim gösterir.
İntegral zamanı, varsayımsal olaylar dizisi sonucu olarak hatanın sıfırdan başlayıp, sabit bir değere birdenbire atladığı durum düşünülerek adlandırılmıştır. Böyle bir hata, denetimcinin oransal teriminden eşzamanlı bir yanıt, ve integral teriminden de sıfırdan başlayıp düzgünce artan bir yanıt gelmesine yol açar. İntegral teriminin, değişmeyen oransal terimi yakalaması için gereken zamana, Ti integral zamanı diyoruz. Uzun integral zamanı olan bir PID denetimci, integrale bağlı tepkiden çok oransal tepki tarafında ağırlık kazanır.
Benzer olarak Td türev zamanı, PID formülündeki türev teriminin göreceli etkisinin bir ölçütüdür. Hata sıfırdan başlayıp sabit bir hızla artmaya başlayacak olsa, türev terimi sabit bir değer alırken, oransal terim sıfırdan başlayacak sonrasında (türev zamanının sonunda) türev terimini yakalayacak şekilde düzgüe artacaktır. Uzun türev zamanı olan bir PID denetimci, oransal tepkiden çok türeve bağlı tepki tarafında ağırlık kazanır.
Tarihsel Notlar
İlk geri beslemeli denetimciler, sadece oransal terimi içeriyorlardı. Sonradan açığa çıkan (matematiksel olarak da gösterilebilen) nedenlere bağlı olarak, bir P-denetimci hatayı küçük fakat sıfır olmayan bir değere kadar düşürüp orada bırakır. Bu durumu gözleyen operatörler, kalan hata kırıntıları da yok edilene kadar denetimci "set değerini" manuel olarak artırırlardı. Bu işleme "denetimcinin tekrar-setlemesi (resetting)" dediler.
İntegral terim ortaya çıktığında, operatörler bu terimin, cihazın tekrar-setlemesini otomatik olarak yapma eğiliminde olduğunu gözlediler. Yani, denetimci hatayı tamamen ortadan kaldıracak kadar oransal tepkisini kaydırıyordu. Bu nedenle integral hareketi ilk zamanlar "otomatik reset" olarak adlandırıldı ve bugüne kadar dahi bazı PID denetimciler bu şekilde etiketlendi. Kısa bir süre sonra türev terimi eklendiğinde de bu sefer doğru olarak "hız kontrolü" şeklinde tarif edildi.
İncelikli Mesele
Proses değişkeninin aşırı salınımlar yapmasına mahal vermeden hatanın ortadan kaldırılması için denetimcinin P, Ti, ve Td parametrelerine değerler seçme sanatına akortlama (ayarlama) denir. Bunu söylemek yapmaktan çok daha kolaydır.
Bir arabanın seyir hızı kontrolünü düşünelim. Denetimci, arabayı istenen seyir hızına ulaşana kadar hızlandırabilir, ama aniden değil. Arabanın ataleti, denetimcinin gaz pedalını devreye alma zamanı ile arabanın hızının set noktasına ulaşma zamanı arasında bir gecikmeye neden olur. Bir PID denetimcinin performansının ne kadar iyi olduğu, büyük çoğunlukla böyle gecikmelere bağlıdır. Fazlasıyla yüklenmiş küçük motorlu bir arabanın birden dik bir tepeye çıkmaya başladığını düşünelim. Arabanın istenen ve mevcut hızları arasındaki bariz hata, denetimcinin türeve bağlı ve oransal tepkilerinin derhal devreye girmesine neden olur. Denetimci aracı (ancak gecikmenin izin verdiği kadar) hızlandırmaya başlar.
Bir süre sonra, integral etkisi de denetimci çıkışına katkıda bulunmaya başlar hatta giderek baskın hale gelir. Çünkü gecikme süresi uzun olduğunda hata o kadar yavaş küçülür ki, ısrarcı bir hata integral etkisini körükleyen bir şeydir. Ama bunun ne zaman ortaya çıkacağı ve integral etkisinin ne kadar baskın olacağı, gecikmenin vehametine ve denetimcinin integral ve türev zamanlarının göreceli büyüklüklerine bağlı olacaktır.
Bu basit örnek, PID akortlamanın temel prensibini gösteriyor. Akortlama parametreleri P, Ti ve Td'nin her biri için en iyi seçimler, hem diğer ikisinin değerlerine hem de kontrollü prosesin davranışına bağlıdır. Dahası herhangi birinin akordunu değiştirmek, diğerlerinin performansını da etkiler çünkü artık prosesi değiştirilmiş denetimci (ve karşılığında proses de denetimciyi) etkilemektedir.
Ziegler - Nichols Akortlaması
Peki bir PID çevrimi tasarlayan kontrol mühendisi belli bir uygulama için en iyi çalışacak P, Ti ve Td değerlerini nasıl belirler. Taylor Instruments'tan (şimdi NY, Rochester'daki ABB enstrümantasyonun parçası) John G. Ziegler ve Nathanial B. Nichols 1942'de bu soruya el attılar ve bugüne kadar gözde kalan iki çevrim-akortlama tekniği yayınladılar.
Açık çevrim teknikleri, geri besleme iptal edilerek denetimcinin çıkışının manuel olarak birden zorla artırıldığı bir tümsek veya basamak testi sonuçlarına dayanır. Proses değişkeninin arkadan gelen yörüngesinin grafiksel dilimi reaksiyon eğrisi olarak bilinir (bkz. Şekil 2). Reaksiyon eğrisinin en dik noktasına teğet çizilen eğimli çizgi, denetimci çıkışındaki basamak değişimine prosesin ne kadar hızlı reaksiyon verdiğini gösterir. Bu çizginin eğiminin tersi, gecikmenin vehametinin ölçütü olan T, prosesin zaman sabitidir. Reaksiyon eğrisi aynı zamanda; proses için, basamağa prosesin başlangıç reaksiyonunu vermesinin ne kadar uzun sürdüğünü (d, ölü zaman) ve basamağın büyüklüğüne göre proses değişkeninin ne kadar arttığını (K, proses kazancı) gösterir. Ziegler ve Nichols deneme - yanılmayla, T, d ve K değerlerinden akortlama parametreleri P, Ti ve Td'nin en iyi değerlerinin aşağıdaki şekilde hesaplanabileceğini belirlediler.
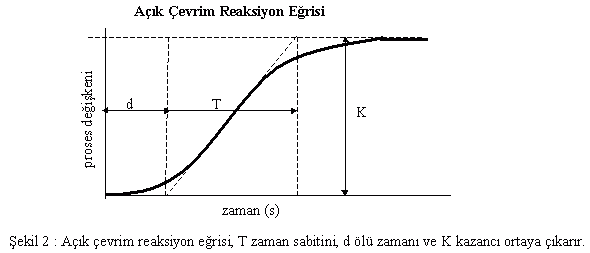
| P = 1,2 T / Kd | Ti = 2 d | Td = 0,5 d |
Bir defa bu parametre değerleri PID formülüne yüklenir ve denetimci otomatik moda döndürülürse, denetimci, proses değerinin aşırı salınımına yol açmadan sonraki hataları ortadan kaldırabilmelidir.
Ziegler ve Nichols ayrıca, denetimcinin otomatik modda fakat integral ve türev hareketlerinin kapatılmış olduğu konumda yürütülecek bir kapalı-çevrim tekniği tarif etmişlerdir. En küçük bir hatanın, proses değişkeninde kalıcı bir osilasyona neden olacağı yere kadar (bkz. Şekil 3) denetimci kazancı artırılır. Böyle bir osilasyona neden olan en küçük denetimci kazancı, nihai kazanç, Pu olarak adlandırılır. Bu osilasyonların periyodu da nihai periyod, Tu, olarak adlandırılır. Uygun akortlama parametreleri, bu iki değere göre aşağıdaki kurallardan hesaplanır.
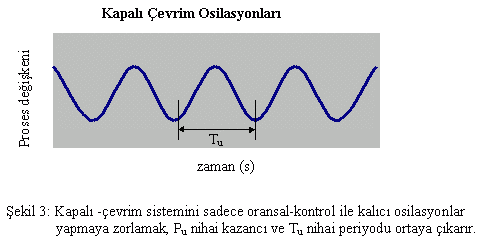
| P = 0,6 Pu | Ti = 0,5 Tu | Td = 0,125 Tu |
Uyarılar
Ne yazık ki, PID çevrim akortlaması bu kadar basit değildir. Değişik PID denetimcileri, PID formülünün değişik versiyonlarını kullanırlar ve her biri uygun kurallar seti doğrultusunda akortlanmalıdır. Kurallar, ayrıca, aşağıdaki durumlarda değişir :
- Türev ve/veya integral hareketi kapatılmış olduğunda,
- Proses kendi yapısı itibarıyla titreşimli/salınımlı ise,
- Proses, sanki kendi integral terimi varmış gibi davranıyorsa (seviye kontrolünde olduğu gibi)
- Ölü zaman d, zaman sabiti T'ye göre çok küçük veya dikkat çekici şekilde büyükse.
Dahası, Ziegler ve Nichols kendi özel akortlama kurallarına odaklandıklarında, akıllarında belli bir kapalı-çevrim performans hedefi vardı. Proses değişkeninde belli bir ölçüde salınımı hoş görmeyi seçtiler, yeter ki sıradaki her tepe kendinden önce gelenin büyüklüğünün dörtte birini geçmesin (çeyrek-dalga-sönümü diye bilinir). Daha da az salınım gerektiren uygulamalar için, akortlama parametrelerine ilave çekiştirmeler gerekir.
İşte çevrim akortlama sanatının başladığı yer burasıdır. Tam doğru P, Ti ve Td kombinasyonuna varabilmek için, birazcık deneyimden daha fazlası ve bol miktarda da şans gerekir.
Neyse ki tüm akortlama kurallarını, tüm değişik PID formülasyonlarını ve tüm güncel akortlama prosedürlerini bilen ticari yazılım ürünleri mevcuttur. Her birinin nasıl çalıştığı bu yazının sahası dışında kalır ve çoğu zaman da sahibinin sırrıdır. Ancak daha fazla bilgi isteyenler, aşağıdaki listeyi kullanabilirler.
- BESTune'dan BESTune.com (www.bestune.isclever.com)
- Control Arts'dan Control Arts PID Tuning Software (www.controlartsinc.com)
- Lambda Controls'dan Control Loop Assistant (www.lambdacontrols.com)
- Control Station Technologies'dan Control Station (www.controlstation.com)
- EnTech Division of Emerson Process Management'dan EnTech Tuner Module (www.entechcontrol.com)
- ExperTune Inc.'dan ExperTune*(www.expertune.com)
- ControlSoft Inc'dan INTUNE* (www.controlsoftinc.com)
- EngineSoft'dan pIDtune (www.pidtune.com)
- Artcon Inc.'dan Pitops (www.artcon.com)
- Techmation'dan Protuner (www.protuner.com)
- ACT. Gmbh'dan TOPAS (www.act-control.com)
- Innovention Industries'dan Tune-Plus (www.innovin.com)
- Plant Automation Services Inc'dan TuneWizard (www.tunewizard.com)
* Bu yazılım paketleri ayrıca, çeşitli denetimci üreticilerinden kendilerinin etiketli ürünleri olarak temin edilebilir.