Bu makale, aşağıda belirtilen kaynaktan Türkçe'ye çevrilmiş ve Bilişim Yayınları / MakinaTek Dergisinin Mart 2006 sayısında yayınlanmıştır. İlgilenenler sorularını bu sitedeki formlarla veya e-posta kanalıyla iletebilirler.
(Kaynak: J.F.W Galyer , C.R.Shotbolt, Metrology for Engineers - Chapter 1, 5th Ed., Cassell Publishers Ltd., 1990)
ÖLÇÜM HATALARI ve BELİRSİZLİK
İhsan Akyüz |
1. Kapsam
Profesyonel uzmanlık alanları ne olursa olsun, tüm teknik kadrolar şu veya bu şekilde sık sık ölçüm sorunları ile karşı karşıya kalırlar. Konu sıcaklığın, elektrik akımının, kütlenin, zamanın, kuvvetin, uzunluğun, açının vb. bir değişkenin veya bunlardan bir kısmının topluca etkisinin ölçümü olabilir. Böyle ölçümlerin sonuçları, neredeyse her zaman, teknik kadroların daha sonra atacağı adımların yönünü belirler. Yani ölçümler vasıtasıyla elde edilen sonuçlar, verilecek kararlara dayanak olan bilgiyi sağlar.
Tüm bu ölçümler, metroloji biliminin parçalarını oluşturur. Mekanik üretimle ilgili teknik kişiler ise özellikle geometrik boyut ölçümleriyle ilgilidirler. Bunlardan uzunluk temel bir öneme sahiptir çünkü açı ve diğer geometrik ölçümler, doğrusal ölçüm kombinasyonlarının uygun olanlarını kullanarak gerçekleştirilebilir.
Öyleyse herhangi bir ölçümün amacı, bir karar verilmesini mümkün kılmaya hizmet etmektir. Bu hizmet, ölçüm kabul edilebilir bir doğrulukta yapılmadıkça tamamlanmış olmayacaktır, ama bilinmelidir ki kusursuz olan bir ölçüm de yoktur. Bu nedenle sadece ölçülen boyutun değil, yapılan ölçüme dair saptananın doğruluk derecesinin de belirtilmesi gereklidir. Ölçme yöntemi bünyesindeki hatalar mümkün mertebe düşük tutulmalı, hata asgariye indirildiğinde de bu asgarinin olası büyüklüğü (veya saptamadaki doğruluk derecesi) belirtilmelidir.
Buradan hareketle, bir mastar blokunun anma değerinin, örneğin, 30 mm. olduğunu söylemek yetmez. Aynı zamanda;
- Blokun ölçülen hatasının, örneğin, - 0,0006 mm.
- Saptamadaki doğruluk derecesinin1, örneğin, ± 0,0004 mm.
olduğunu da söylemek gerekir.
Bu bilgiye sahip olan kullanıcı, artık gerektiği yerde onu kullanacaktır. Eğer söz konusu mastar bloku, yalnızca 0,02 mm.'ye kadar okunabilen bir mihengirin kıyas seviyesini tayin etmekte kullanılacaksa, mastarın hataları ihmal edilebilecek kadar küçük kalır. Diğer yandan, skala taksimatları 0,001 mm.'yi gösteren bir komparatörü hazırlamakta kullanılacaksa, o zaman ölçülen hata gözönüne alınacak kadar belirgindir ve mastar blok ölçümünde ortaya çıkan hatalar, komparatörle yapılacak kıyaslamaların doğruluk derecelerine dahil edilmelidir.
________________________
1Burada "saptamadaki doğruluk derecesi" olarak ifade edilen kavramın, bugünkü terminolojide "ölçüm belirsizliği" terimi ile tanımlanmış olduğunu ifade etmek yanlış olmayacaktır. Bu nedenle kavram karışıklığı yaratacak bir eski terim kullanmaktansa, buradan sonraki bölümlerde orjinal metindeki "saptama doğruluğu"nun yerine "ölçüm belirsizliği" ifadesi kullanılacaktır.
2. Hata Tipleri
Genellikle herhangi bir ölçümde ortaya çıkan hataları, iki ayrı tipten biri olarak düşünebiliriz; normalde olmaması gereken, özenli çalışarak ve ayrıntılara dikkat ederek giderilebilenler ile, ölçme işleminin doğasında kaçınılmaz olarak mevcut olanlar.
2.1 Büyük Oranda Giderilebilen Hatalar
2.1.1 Yıkıcı (Vahim) Hatalar
Bunlar iki temel nedeni olan büyük boyutlu hatalardır:
- Yanlış okuma.. Doğru değer olan 5,28 mm.'nin, bir mikrometre ile 6,28 mm. veya 5,78 mm. şeklinde yanlış okunması gibi.
- Aritmetik hataları.Çoğunlukla toplama hatalarıdır. En basit kontrol, yapılan hesaplamaların ikinci defa farklı bir yöntem kullanarak yapılması şekliyle olabilir, örneğin, bir sütundaki sayıları sonuçların çakıştığından emin olmak üzere iki kere toplamak; birincisi yukarıdan aşağıya ikincisi aşağıdan yukarıya.
Çoğu durumda böyle hatalar beklenenden o kadar farklı sonuca yolaçarlar ki, bir hata oluştuğu barizdir ve ölçüm tekrarlanarak hata tesbit edilir. Ne yazık ki her zaman da böyle olmaz, ve bu tip hatalar ancak ve ancak özenli çalışma ve ayrıntılara dikkat etme sayesinde önlenir.
2.1.2 Hizalama/Konumlama Hataları
Bu tip hata, ölçü aleti iş parçasına göre yanlış hizalandığı/yerleştirildiği durumlarda oluşur. Genellikle ölçülen M boyutunun, gerçekteki D boyutu ile bir trigonometri oranıyla ilişkilendirildiği sonuçlara yolaçar. Dolayısıyla trigonometrik hata veya kosinüs hatası diye bilinir. Bir ölçü saatinin gereken ölçüm doğrultusuna göre q açısı kadar eğik konumlandığı bir basit örnek Şekil 1'de gösterilmiştir. Burada;
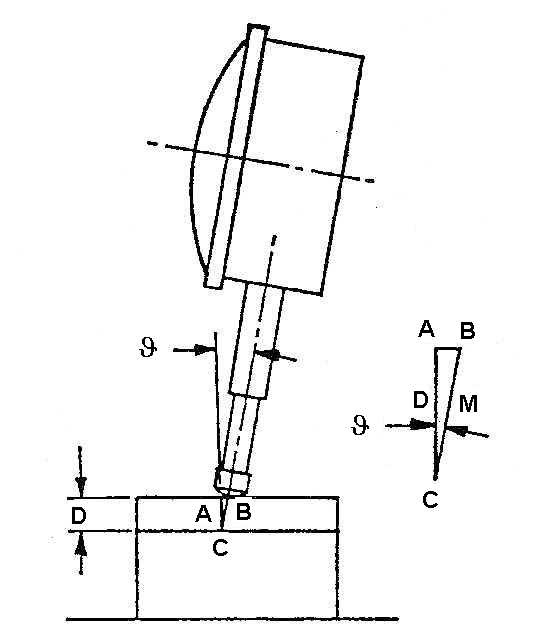 D = M cosq
D = M cosq
Bu hatanın bir başka şekli, Şekil 2'de görülen, bakma doğrultusunun cihaz skalasına dik olmadığı (ölçülen kenar-skala işareti-göz veya skala işareti-ibre-göz aynı çizgide olmadığı) durumdaki paralaks yanılgısıdır.
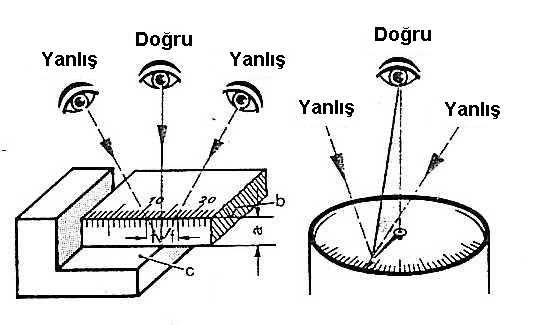
Bu ibreli enstrümanlarda yaygın görülen okuma hatası, skala üzerine yansıtıcı bir şerit konarak bertaraf edilmektedir. Bu takdirde, göz ve ibre arasındaki hayali çizgi, ancak ibrenin şerit üzerindeki yansımasını kapatacak açıdan bakılırsa, skalaya tam dik olmaktadır.
2.1.3 Ortam Koşullarından Kaynaklanan Hatalar
Ölçümlerin çoğu az ya da çok, içinde yapıldıkları çevreden etkilenirler. En önemli koşul, hem iş parçasının hem de çevresinin sıcaklığıdır. Uluslararası standart sıcaklık (geometrik boyutların ölçümünde) 20°C'dir ve ortam sıcaklığı da bu seviyede tutulmalıdır. Bu ne kadar titizlikle kontrol edilirse edilsin, iş parçasının sıcaklığı değişmeye açıksa (ortamdan farklı sıcaklıktaysa) yararı olmaz. Bir mastarın elde tutulması onun sıcaklığını değiştirir, öyleyse mümkün olduğunca az ellenmeli ve elde tutulduktan sonra da termal dengeye gelmesi beklenmelidir. Ölçümler yüksek seviyede bir doğrulukla yapılacaksa, bir mastarın her 25 mm.'lik boyu başına 20 dakika tavsiye edilir. Plastik veya tahta bir masa üstü yerine, en iyisi bir ölçüm sırasında kullanılacak bütün parçaların döküm demir (veya granit) pleyt üzerinde beklemeye bırakılmasıdır. Döküm demir iyi bir iletken olduğundan, bir ısı havuzu görevi yaparak sıcaklık farklarını daha hızlı yok eder. Sıcaklığın etkileri tartışılırken, gözönüne alınacak iki durum vardır:
(a) Doğrudan ölçüm. İnterferometre vasıtasıyla doğrudan ölçülen bir mastar blok düşünelim. Burada standart dışı bir sıcaklıktaki ortam, aşağıdaki gibi doğru orantılı hataya yolaçar.
Hata = l a (t - ts)
l = anma boyu
a
= genleşme
katsayısı
(t - ts) = standart sıcaklıktan sapma
(b) Kıyaslamalı ölçüm. Eğer genleşme katsayıları sırasıyla a 1 ve a 2 şeklinde farklı olan iki mastar düşünürsek, bu durumda standart dışı bir sıcaklığın yolaçacağı hata şöyle olacaktır:
Hata = l (a 1 - a 2) (t - ts)
Genleşme katsayıları küçük rakamlar olduğundan, her iki parça da aynı sıcaklıkta olduktan sonra, hata çok küçük olacaktır. Öyleyse kıyaslamalı ölçümlerde, ölçme sistemindeki tüm parçaların standart sıcaklıkta olmaları şart olmayıp, hepsinin aynı sıcaklıkta olmaları önemlidir.
Diğer ortam koşulları da ölçüm sonucunu etkileyebilirler. Eğer bir mastar bloku interferometre vasıtasıyla ölçülüyorsa, bağıl nem, atmosferik basınç ve havadaki karbon dioksit oranı atmosferin kırılma indisini etkiler. Tüm bu koşullar işlem sırasında kaydedilmeli ve gereken düzeltmeler yapılmalıdır.
2.1.4 Elastik Deformasyondan Kaynaklanan Hatalar
Bir yüke maruz kalan her elastik nesne, elastik deformasyona uğrar. Deformasyonun miktarı; yükün miktarına, temas alanına ve temas halindeki malzemelerin özelliklerine bağlı olacaktır. Bu nedenle kıyaslamalı ölçümlerde ölçme kuvvetlerinin aynı olmasını sağlamak gereklidir.
Komparatörler, tezgah mikrometreleri gibi hassas ölçümde kullanılan aletlerde, ölçme baskısı sabit sayılabilir ama asıl zorluk, bir aleti mastarla ayarlarkenki ile sonrasında iş parçası üzerinde okuma yaparkenki temas tiplerinin farklı olmasından kaynaklanır. Buna çarpıcı bir örnek, bir vida dişinin efektif anma çapının ölçümünde, ayarlama mastarı iki noktadan temas gerektirirken, vida dişinin V-formunda dört noktadan temas gerektirmesidir. Gereken doğruluğun düzeltme gerektirmesi halinde kullanılmak üzere düzeltme tabloları yayınlanmıştır.
Çapları değişik ve E, elastik modül, v, Poisson oranı olmak üzere elastik özellikleri farklı malzemeden parçalar arasında yüksek doğruluk derecesiyle kıyaslama yapılacaksa, ölçme ucunun ayarlama mastarı ve iş parçası ile temas ettirilmesiyle oluşacak elastik deformasyonlardaki fark için düzeltmeler yapılabilir.
S. Timoshenko'nun çalışmasından alınan aşağıdaki ifade, W baskısıyla biraraya getirilen bir küresel uç ile bir küresel yüzey arasındaki deformasyonu yani merkezler arası uzaklığındaki değişmeyi tarif eder.
Toplam deformasyon d = 1,774 W 2/3 (k1 + k2) 2/3 (1/R1 + 1/R2) 1/3
öyle ki R1 = mastar yarıçapı R2 = ölçme ucunun yarıçapı
ve k1 = (1 - v12) / E1 k2 = (1 - v12) / E1
Eğer kıyaslamalı ölçüm, komparatörün bir A mastarı ile ayarlanması ve bir B mastarı üzerinden ölçüm alınmasını içeriyorsa, ortaya çıkan hata, k1, k2, R1, R2 yerine d formülüne hem A hem B durumu için uygun değerlerin yerleştirilmesiyle (d A - d B) şeklinde bulunacaktır.
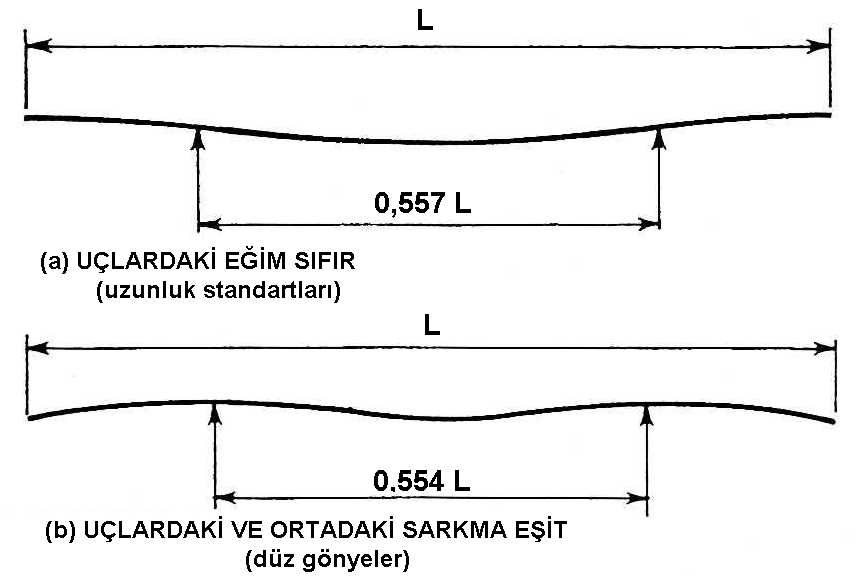
Elastik deformasyonun başka bir biçimi, bir nesnenin kendi ağırlığı altında sarkmasıdır. Bu sorun, dayanakların konumlarının bir minimum hata verecek şekilde düzenlenebileceğini göstermiş olan G.B. Airy tarafından incelenmiştir. Şekil 2'de gösterilen iki koşul ele alınmış olup, birisi çubuğun uçlarındaki eğimin sıfır olduğu, diğeri uçlardaki sarkmanın ortadaki sarkmaya eşit olduğu durumdur. Uzunluk standartları söz konusu olduğunda çubuğun kesiti H şeklindedir ve skalası nötral eksen düzleminde bir yüzeye işlenmiştir. Böylece sarkmaya bağlı elastik deformasyon, skala bölümlerinin uzunluğu üzerinde asgari etkiye sahiptir.
2.2 Giderilemeyen Hatalar
Kesin boyutu verecek bir ölçüm yapılamaz. Temelde bunun nedeni, nihayetinde kaydedilen değerin insan gözünün bir skalayı okumasına bağlı oluşudur. Bu nedenle okuma, sonuçtaki doğruluğunun skalanın doğruluğuna, operatörün skalayı okuma yeteneğine, ve bazı durumlarda operatörün dokunma hassasiyeti ya da hissiyatına bağlı olduğu bir tahmindir.
2.2.1 Skala Hataları
Eğer bir ölçümün dayandığı skala hatalıysa, elbetteki o ölçüm hatalıdır. Bunun ancak, cihaz skalasının tüm boyunun değeri bilinen uzunluk standartları kullanılarak kalibre edilmesiyle üstesinden gelinebilir.
Kıyaslamalı ölçümlerde, kontrol edilen mastarın boyuna olabildiği kadar yakın bir ayarlama mastarı seçip, mümkün olduğunca kısa skala boyları kullanılarak, skala hatalarının etkileri azaltılabilir.
2.2.2 Okunabilirlik Hataları
Bir skala ne kadar incelikli (hassas) okunabilir? Bu cetvel çizgilerinin kalınlığına, skala taksimatlarının aralığına ve ibrenin ya da kıyas noktasının kalınlığına bağlıdır.
Bir rehber olarak, ibre ya da kıyas noktasının bir skala taksimatıyla çakıştığı durumda, skala taksimatının % 10'u mertebesinde doğru okunabileceği kabul edilir. Diğer taraftan, ibre konumunun taksimatların arasında kaldığı durumun tahmini daha düşük doğruluklu olup, skala taksimatının ± % 20'si alınmalıdır. Yani bölüntüleri 0,001 mm'ye denk gelen bir skaladan yapılan - 3 birimlik okuma, ± 0,0001 mm ölçüm belirsizliği olan - 0,003 mm.'lik bir kıyaslama ölçümü demektir. Oysa ölçüm - 3,4 birim olsaydı, - 0,0034 ± 0,0002 mm. anlamına gelecekti.
Ölçüm bir komparatörle yapılıyorsa unutulmamalıdır ki bu çeşit hata, birincisi cihaz mastar ölçekle ayarlanırken, ikincisi iş parçasından ölçüm alınırken olmak üzere iki defa oluşur.
2.2.3 Ölçme Hataları
Yukarıda anlatılan değişik tip hatalar kümülatiftir ve bazı durumlarda temas duyarlılığı ya da hissiyatı için bir miktar daha eklenmelidir. Bu kullanılan cihaza bağlı olacaktır ve genelde komparatörler için bu etki giderilmiştir.
Şimdi anma çapı 25 mm. olan düz bir tampon mastarın hatasının ölçümünü düşünelim. ± 0,0002 mm.'lik doğrulukla saptanmış - 0.0001 mm.'lik bilinen hatasıyla nominal değeri 25 mm. olan bir mastar blokla ayarlanmış ,büyütme faktörü 5000x olan bir komparatör kullanılarak ölçüm yapılacaktır. Mastar blok üzerinde alınan ölçüm 0 skala bölüntüsü, tampon mastar üzerinde alınan ölçüm - 1,2 skala bölüntüsüdür.
Bu örnekte temas koşulları biraz farklıysa da, iki parça benzer baskı altında ve benzer malzemeden olduğundan elastik deformasyon etkisi ihmal edilebilir. Problem bir tablo halinde aşağıdaki şekilde sunulabilir.
| Hata Elemanı | Okunan Miktar | Ölçüm Belirsizliği |
| Mastar blok Komparatör ayarı Komparatör okuması |
- 0,0001 mm 0 - 0,0012 mm |
± 0,0002 mm ± 0,0001 mm ± 0,0002 mm |
| Toplamlar | - 0,0013 | ± 0,0005 mm |
Sonuçta mastar büyüklüğü 24,9987 mm bulunmuştur ama ölçümdeki belirsizlik miktarı gösteriyor ki 24,9992 mm ile 24,9982 mm arasında herhangi bir yerde olabilir. Gerçekte ölçüm belirsizliğinin ± 0,0005 mm'den daha iyi olacağı özet bölümünde gösterilmiştir.
3. Bileşik Hatalar
Sonuçta hesaplanan ölçümün, d a , d b , d c, vb. bireysel belirsizliklere sahip a, b, c, vb. birkaç bireysel ölçümün fonksiyonu olduğu birçok durum oluşmaktadır. Bu durumda M'nin ölçüm belirsizliğini (dM ile gösterebiliriz) bulmak için M'nin formülüne a, b, c, vb.nin maksimum ve minimum değerlerini koyup M'nin maksimum ve minimum değerlerini hesaplayabiliriz.
Açıktır ki bu biraz zahmetli bir iş olacaktır ve problem, kısmi türev alınması ile daha iyi çözülür.
Kısmi türev kuralına göre dM = (¶ M / ¶ a ) d a + (¶ M / ¶ b ) d b + (¶ M / ¶ c ) d c +
burada (¶ M / ¶ a) tüm diğer değişkenler (b, c, ) sabit tutulduğunda M 'nin a 'ya göre türev katsayısıdır.
aynı şekilde (¶ M / ¶ b ) M 'nin b 'ye göre, (¶ M / ¶ c ) M 'nin c 'ye göre vb.
4. Ortalama Almanın Etkisi
Ölçüm belirsizliği, bir ölçümün doğru değerinden sapabileceği miktarın kestirilmesi olup, muhakkak saptığı anlamına da gelmez. Tesadüfi olarak ölçüm tam doğru olabileceği gibi, ölçüm belirsizliğinin herhangi bir kesri kadar doğru değerden sapmış da olabilir. Bunu bilmenin, daha iyi (küçük) belirsizliğe sahip bir ölçme yöntemi kullanmaktan başka yolu yoktur.
Tüm ölçümü birçok defa tekrarlarsak, ölçülen x büyüklüğü için farklı değerlerde rakamlar elde ederiz. Bu verileri kullanarak standart sapma s 'yı hesaplayabiliriz. Biliyoruz ki ölçümlerin %99 küsuru gözlemlerin ortalamasının ±3s yakınında yatmaktadır, öyleyse pratik amaçlar için ölçüm belirsizliğinin ±3s 'ya eşit olduğunu söyleyebiliriz.
Şimdi de gözlemlerimizi rasgele n adet alt-kümeye bölüp, her küme için onun ortalaması xm'yi hesaplayarak xm değerleri için bir dağılım oluşturabiliriz. Biraz düşünürsek bu dağılımın asıl ortalama etrafında önceki bireysel verilere göre daha yakın toplanacağını tahmin edebiliriz.
Gösterilmiştir ki;
n ; alt-küme veya örnek sayısı ve
s
; bireysel
verilerin standart sapması iken,
xm ortalamalarının standart
sapması s m = s / Ö n bağıntısı
ile bulunur.
Buradan da, n adet gözlemin ortalama büyüklüğünün belirsizliği ± 3s m veya ± 3s / Ö n olacaktır.
İstatistiksel tablolar tüm gözlemlerin yaklaşık %95'inin, gözlemlerin ortalamasının ± 2s yakınında ve yaklaşık %68'inin, gözlemlerin ortalamasının ± 1s yakınında yattığını söylemektedir. Biz de artık ölçüm belirsizliği ile birlikte vereceğimiz güvenilirliği belirtebiliriz. Şimdi tek bir gözlemin tahmin edilen belirsizliği ±d olsun. Bu ± 3s 'ya denk geldiğinden, tüm benzer gözlemlerin %99'dan fazlası için bu ölçüm belirsizliğinin geçerli olacağına güvendiğimizi söyleyebiliriz. Basitçe, diyoruz ki ± d bizim %99 güvenilirlik limitimizi ifade eder. Benzer olarak ± 2s = ± 2/3d bize %95 güvenilirlik limitlerimizi, ve ± 1s = ± 1/3d bize %68 güvenilirlik limitlerimizi verecektir.
Eğer bunu n adet gözlemimizin ortalamasına uygularsak;
%99 güvenilirlik limitleri = ± d / Ö n ,
%95 güvenilirlik limitleri = ± 2d / 3Ö n ,
%68 güvenilirlik limitleri = ± d / 3Ö n olur.
Bunu doğru olarak yapmak için çok sayıda gözlem yapmalı ve bunlardan standart sapmanın gerçek değerini hesaplamalıyız, ama belirsizliği kestirirken sadece onun değerini değil o değere atfedilen uygun güvenilirlik derecesini de vermeliyiz.
5. Grafiksel Yöntemler
Ölçülen iki değişkenin birbirleriyle ilişkisini ifade eden bir kural bulunmasına yönelik bir deney yapıldığında, yaygın olarak alınan ölçümler doğrultusunda bir grafik çizilir ve grafiğin kuralı bir ortalama çizgi geçirilerek (dolayısıyla bireysel ölçümlerdeki hatalar dışlanarak) belirlenir. Genellikle gözlemler, çizginin eğiminin a, ve y-ekseni kesişiminin de b olduğu y = ax + b formunda bir doğrusal grafik verecek şekilde hesaplamaya alınır. Eğer çizgi, gözle kestirim yapacak şekilde grafiğe çizilirse, sonuç halen hataya açık olacaktır. Eğer her noktada bireysel gözlemlerin ölçüm belirsizliğine denk gelen bir dikdörtgen çizilirse, bu sefer en kenarda kalan uçlardan geçen iki ayrı çizgi çizilebilecek ve iki kural bulunacaktır. Bunlar aranan kuralın belirsizlik sınırlarını verecektir. Açıkcası bu yorucu bir iştir ve en küçük kareler yöntemi adlı daha basit bir yöntem bilinmektedir.
En küçük kareler yöntemi
Grafiğin eğimi olan a'yı alalım. Bu x'deki belli bir dilim artışa karşılık, y'deki ortalama artma anlamına gelir ve şöyle ifade edilebilir:
a = S (x - xm) (y - ym) / S (x - xm)2
a için en iyi değer bulunduğuna göre, b'nin en iyi değeri de aşağıdaki doğru denklemine x ve y ortalamalarını koyarak bulunabilir.
ym = axm + b ym = S y / n xm = S x / n
Problem en iyisi tablo halinde kurulabilir ve yukarıdaki formüllerden görüldüğü üzre gözlenen değerler x ve y'nin yanında, ortalamalar, ortalamadan farklar ve bunların toplamları için bazı ek satır ve sütunlara da ihtiyaç olacaktır. Ağağıda verilen deneysel değerleri alalım:
| S | ort | ||||||||||||||
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 91 | 7 |
| y | 17 | 18 | 24 | 31 | 33 | 37 | 33 | 36 | 41 | 44 | 57 | 57 | 54 | 481 | 37 |
| (x - xm) | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ||
| (y - ym) | -20 | -19 | -13 | -6 | -4 | 0 | -4 | -1 | 4 | 7 | 20 | 20 | 17 | ||
| 120 | 95 | 52 | 18 | 8 | 0 | 0 | -1 | 8 | 21 | 80 | 100 | 102 | 603 | ||
| (x - xm)2 | 36 | 25 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 182 | |
a = S (x - xm) (y - ym) / S (x - xm)2 = 603 / 182 = 3,31 a = 3,31
ym = axm + b 37 = (3,31) 7 + b b = 13,83
Bu örnekteki düz çizginin kuralı öyleyse y = 3,31 x + 13,83 şeklindedir.
Şimdi x değerlerini yukarıdaki denkleme yerleştirirsek Y olarak gösterebileceğimiz teorik y değerlerini bulabiliriz. O zaman gözlemlerdeki hata (y - Y) olacaktır.
Düzlük ve düzlemsellik testlerinin değerlendirilmesinde bu yöntemin kullanılması önerilmektedir.
6. Özet
Burada anlatılanlardan çıkarılacak temel noktalar aşağıdaki gibi özetlenebilir:
- Tüm ölçümlerde hata vardır.
- Belirtilen ölçümden olası sapma kestirilmeli ve "ölçüm belirsizliği" olarak verilmelidir.
- Ölçüm belirsizliği, ölçümü birkaç defa tekrarlayıp ortalamayı belirtmek suretiyle iyileştirilebilir.
- Ölçü belirsizliğini, belli bir güvenilirlikle birlikte ifade etmenin istatistiksel yolları mevcut olup, bunlar anlaşılmalı ve kullanılmalıdır.
- İstatistiksel yöntemler, normalde grafiksel olarak ifade edilen deneysel verilerin analizi için de uygulanabilir ve genellikle bu yöntemler, deneysel verileri sonradan çıkarılacak kurallara daha iyi oturturlar.
Ölçme hataları ile ilgili bölümde (2.2.3) hesaplanmış olan ölçüm belirsizliği olası en kötü duruma denk düşmektedir. Oradaki örnekte, her biri için belirsizliği d 1, d 2, d 3 olmak üzere, ölçümün üç elemanı vardır:
- mastar bloku,
- komparatör düzeneği,
- komparatörden okunan.
Hesaplanan ölçüm belirsizliği, tek tek belirsizliklerin ± (d 1 + d 2 + d 3) şeklinde aritmetik toplamı idi.
Aslında açıktır ki d 1, d 2, d 3'ün hepsinin artı ya da eksi olma şansları eşittir ve herhangi birinin veya hepsinin maksimum değerde olma olasılığı düşüktür. İstatistiksel olarak ölçüm belirsizliğine dair daha iyi bir tahmin şöyle verilmektedir:
ölçüm belirsizliği = ± Ö (d 12 + d 22 + d 32)
= ± 0,0001Ö (2 2 + 1 2 + 2 2)
= ± 0,0003 mm